每年學校的清明節與復活節假期都會很相近,學校大多將它們編在一起。但今年的復活節特別晚,究竟為何呢?當中與數學又有何關係呢?
清明節的計算
清明節跟端午節和中秋節不同,它沒有固定的日子。這是因為清明節是二十四節氣之一,其計算的方法是按照太陽在天空中運行的真實位置而定,即冬至後105天。節氣會被每四年一次的閏年影響,每四年會多閏日一天,所以差異也只會是三天內,這就是清明節總會在4月4日至6日之間的原因。
清明節的計算公式:
int[Y*D+C]-L
Y代表年數的最後2個位(如2019年即19),D=0.2422(一個回歸年實際長度為365.2422天,以365天計算,所以每年多0.2422天),L=閏年數,21世紀C=4.81,20世紀=5.59。
Int 是取數字的整數部分(如 4.75 取為4)
舉例:2019年清明日期=int[19×.0.2422+4.81]-int[19/4]=9-4=5,4月5日是清明。
復活節的計算
每年的復活節都是在3月至4月間,但每人年的日子也不相同,時在3月尾,時在4月初,今年更在4月中旬後。究竟背後不解之謎是什麼呢?《聖經》或其他文獻都沒有記載耶穌被釘十字架和復活的日期。但按《聖經》福音書所記,從耶穌被賣前和門徒作最後晚餐的時間上得知,當時正是在慶祝猶太教的逾越節。由於猶太曆法與羅馬帝國分別以陰曆及陽曆為依據,因此復活節的計算方法,就存在着不同的說法。以下是其中的兩個計算方法:
一、猶太及小亞細亞早期教會傳統,以尼散月14日為復活節
二、小亞細亞以外的教會,以尼散月14日後首個主日為復活節,即陰曆春分月圓後的第一個主日。
最終在公元325年舉行的尼西亞大會,議定復活節為星期日,並訂定以春分月圓後第一個星期日為復活節。但由於每個國家及民族的陽曆仍有差異,所以在尼西亞大會後,計算出的日子依然未能統一。直至公元1582年,格雷戈里曆(Gregorian Calendar)的改良版在歐洲普及後,復活節的日期才得以統一。復活節現代的計算方法是3月21日後月圓出現後的星期日。以今年為例子,3月21日為半月,之後的滿月是4月18日為星期四,所以復活節就定在之後的星期日4月21日。
要數復活節與數學的關係,怎能不提以著名數學家高斯Johann Karl Friedrich Gauß命名的高斯演算法。我們可以高斯演算法計算出復活節的日期,方法如下︰
用Y表示年份及參照以下的對算表及公式,便能計算出復活節的日期。
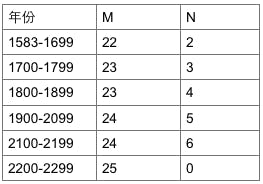
公式︰
a = Y mod 19
b = Y mod 4
c = Y mod 7
d = (19a + M) mod 30
e = (2b + 4c + 6d + N) mod 7
mod運算指整數除法的餘數(例如14 mod 5 = 4)
法則︰
若d+e < 10則復活節在3月(d+e+22)日,反則在4月(d+e-9)日,
除了以下兩個特殊情況:
若公式算出的日期是4月26日,復活節在4月19日;
若公式算出的日期是4月25日,同時d=28、e=6和a>10,復活節應在4月18日。








































