本周五是冬至,中國人一向視「冬大過年」,先祝各位讀者平安。上文提及的機率論,收到很多讀者詢問,為什麼擲公字不是隨機? 為什麼連續數字的機率都不是按公式計算的結果呢?
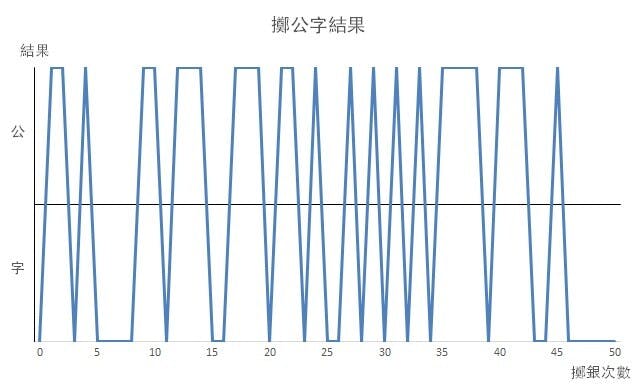
圖一及圖二,是工作人員協助下,連擲一千次公字的結果。圖一在150次至250次形成了下跌趨勢!之後由250次左右開始上升至680次左右,之後高位橫行至800次左右下跌。由250次開始出現升──橫行──跌,這便是一個生成元,而很多小的生成元,便合成一個大的生成元,最終形成了一次大的周期。這便是碎形理論對市場的基本論述。圖二由180次左右開始上升至300次左右見頂橫行,在500次左右見頂回落,同樣形成了生成元。兩者都是人手逐次擲公字的結果,而兩者所構成的圖象不同,正是隨機因子作怪。


「市場時而沉靜,時而狂野,而且狂野的程度不同,便有不同分布,故此,價格並不存在常態分布的關係,最重要的是按時間推移,市場根本不存在任何一種固有的分布形態,這也是說明簡單基本的回歸分析,雖在邏輯上正確,但仍未可成功捕捉市場走勢的原因所在。」
事前機率vs事後機率
早年美國有一本著作,為市場帶來不少迴響,這就是由Nate Silver所著的精準預測。書中提到貝氏定理Bayes’ theorem的應用。筆者查看相關文獻,竟然找到一些美國法院文件,有不少案件都對貝氏定理的推論有懷疑!其中一個爭議之處,便是貝氏本人從來都沒有發表過一篇科學文章。現時頻率機率論的學者,引用的貝氏定理主要是參考1763年12月23日由數學家普萊斯(Richard Price)在英國皇家學會宣讀一篇貝氏的論文,當時貝氏已離世四個月。普萊斯宣稱是貝氏的遺囑託付給他,文章題目為〈關於解決機率論的一個難題〉。亞當史密斯的國富論初稿,也是由普萊斯作為初審,而精算學的基礎理論也是由普萊斯的名著〈分紅給付〉一書中確立。
由這樣鼎鼎大名的人物發表的貝氏定理,自當舉世矚目。貝氏主要是處理條件機率問題,跟白努利一樣,想藉在無限多的數據中觀察一部分而得知整體出現的機率。前文已述白努利的處理方法,本文便介紹貝氏的處理方法。統計學大師、Nate Silver的老師Leonard Mlodinow在與物理學大師霍金合著的作品中,曾如此說明貝氏理論,假設現時在玩草地滾球,我們先把第一顆球滾出去,使它在草地上任何一點停止的機率都一樣。而就在不經觀察的盲測下,決定球的水平軸在何處停下來,而測試的工具便是第二顆球,只要多次滾動第二顆球,再記錄數據,第一顆球就是未知事件,而第二顆球就代表我們收集到的證據。如果第二顆球一直都在第一顆的右邊,我們便可假設第一顆球非常接近草地的左邊界。第一顆球的估計位置,被稱為事前機率,而用第二顆球的位置來修正第一顆球的位置,稱為事後機率。
貝氏定理在計算時其實蠻複雜的,主要是倚靠新的數據去修正結果,提供的樣本愈多,機率也隨之改變。定理指出,假如B已發生則A又發生的機率,並不等於假如A發生而B又同時發生的機率。90年代有一宗個案值得跟大家分享,按美國及德國的聯合調查,研究員請醫生評估40-50歲女性無乳癌但X光造影中顯示為陽性的、確實患乳癌的機率。研究員事前已知當中有7%女性並無患上乳癌,他們告知這批醫生,所有40-50歲婦女平均患上乳癌的機率是0.8%,而X光造影顯示為陽性之後,假陰性的機率是10%。但德國的醫生有三分之一估計當中有90%的婦女患上乳癌,而平均值是70%,而美國醫生有95%估計這批婦女中有75%患上乳癌。
貝氏定理,在實際運用上頗有後見之明,在美國總統大選中, Nate Silver便計出希拉莉預期會得到七成的選票,並在選舉人票中輕微多於特朗普可以入主白官,結果當然出錯了。去到這個關口,統計學中的預測學,跟物理學的量子模型漸漸分道揚鑣,下篇文章筆者會跟大家分享兩者後續的發展,以及如何在股票市場中大放異彩。






































