凱因斯認為機率是有邏輯的,並提出「無差異原則」。 現在以3月5日〈運籌帷幄論決策〉一文中的例子作討論:
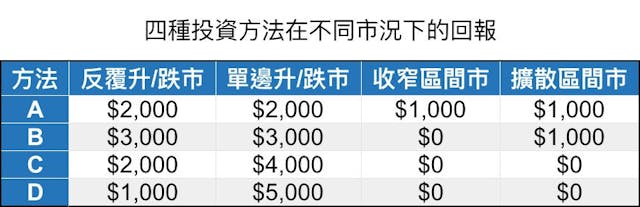
假設四種市況發生的機率一致,亦即25%,在主觀機率的分配下,四種方法的利潤期望值如下:
方法A: $2,000 X 25% + $2,000 X 25% + $1,000 X 25% + $1,000 X 25%= $1,500
方法B: $3,000 X 25% + $3,000 X 25% + $0 X 25% + $1,000 X 25%= $1,750
方法C: $2,000 X 25% + $4,000 X 25% + $0 X 25% + $0 X 25%= $1,500
方法D: $1,000 X 25% + $5,000 X 25% + $0 X 25% + $0 X 25%= $1,500
如果以這種思考模式,在期望值的準則下,採用方法B是最理想的。
邏輯推論分配
凱因斯在二十世紀初環球經濟大蕭條下,提倡財政及金融政策有效性的經濟學家,如細閱其論文,有點像熊彼得的創見卻又不盡然。如大家有看投資類書籍的習慣,書店有不少書籍都會比較奧地利學派巨匠海耶克及凱因斯的分別。
凱因斯的博士論文〈機率論〉被認為是將機率思考,由數學機率、統計機率推展至主觀機率的先驅研究。凱因斯認為機率是有關連性,提出〈因A則B〉的因果相連原則及〈若A則B〉的推論原則。以上述例子的四種市況來說明,凱因斯將「市況發生的機率為25%」定義為,「經過邏輯對比不同數據後,某一種市況發生的機率可信度為25%」這種可信度或信念的數值。
凱因斯將這種把可信度量化為數值的概念,推演成「無差異原則」,所以儘管市況將會上升,但會是急升還是慢升,在邏輯上並無得到支持,反過來說,任何市況出現的可能性應該一樣。
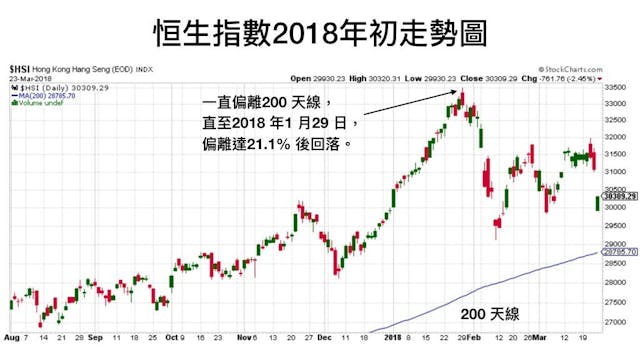
後續的計量分析研究認為,凱因斯成功解釋了市場短期的隨機漫步,但對中長線的市場趨勢卻未能解釋。不過,凱因斯的理論對操作上便饒富意義,筆者同樣以2018年1月下旬的數據分析,當時大市已偏離200天移動平均線達20%,已屆回套邊緣,當時大家都了解大市勢必出現回歸均值的情況,但究竟會以哪種形式回歸卻並不知道。由於理論上已偏離200天移動平均線20%,再升的機率應極低,但事實上大市卻最終偏離21.1%才回落,因為短線而言,升跌的機率相當。
2011年,日本發生311大地震,在地震發生前大市只是橫行,當然亦沒有人可以預知將會發生大地震。地震之後大市反覆下跌,在3月15日,恆生指數已大跌至22253點,當時大市已出現深度超賣,筆者以向心系統計算當時已大幅偏離均值,料日內反彈機率已達92%,屬相當高的水平,便買入4月22600點的認購期權。
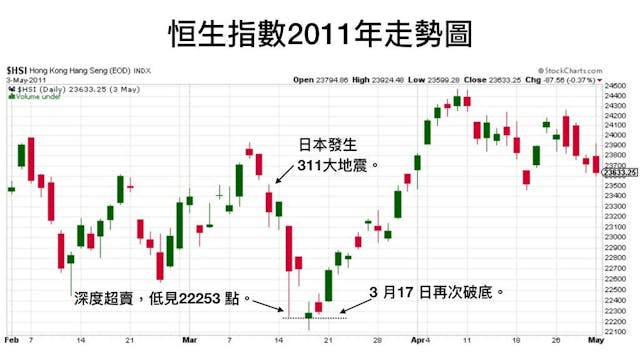
可惜天不如人願,大市進一步下跌至3月17日,低見22123點才見底。跌穿了3月15日的底部,當年操作的功力不及今天深湛,跌穿了22253點時,心理也感到一絲擔憂,當時先把LC22600平倉,靜心再計算一下。15分鐘後,便決定再次建倉,可惜當時已高於剛才的平倉價,結果是在低位平倉,在稍高位置回補。當時靜心計算,既然因超賣而買入,而現時更加深度超賣,所需要的不是加倉,增加風險;也不是減倉,不信任計算結果,始終長時間累積下來,會得到計算值應有的成功機率。筆者需要的正是對系統的信任,及維持操作系統的穩定性。最終筆者在4月24200點左右水平鎖倉,大賺近八倍回報。