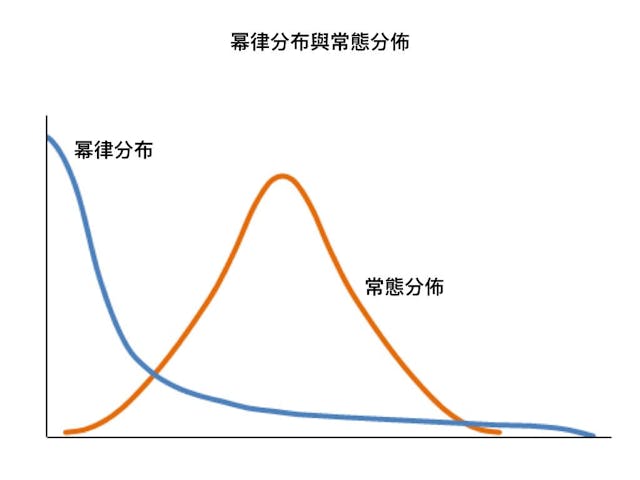
之前的文章,集中討論了條件機率,大數法則及大市的非常態分布。今天跟大家談的是第四條重要法則, 中央極限定理(central limit theorem)。以擲骰子為例,我們擲骰子10次後計算其平均值,之後再擲10次,再計算平均值, 經過無數次之後,每次組成的數字排列都不同,但平均值卻變化不大。而在無數次投擲之後,我們會得到一系列的平均數。
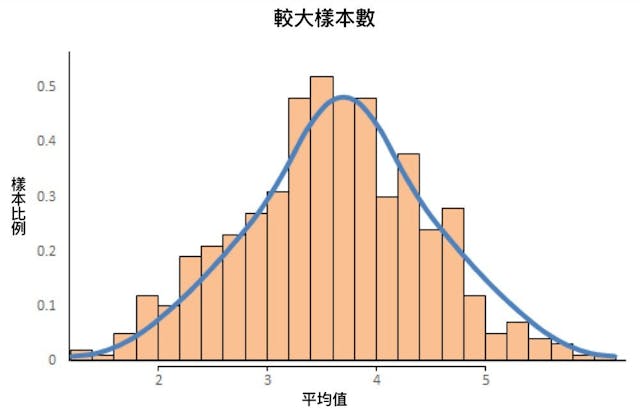
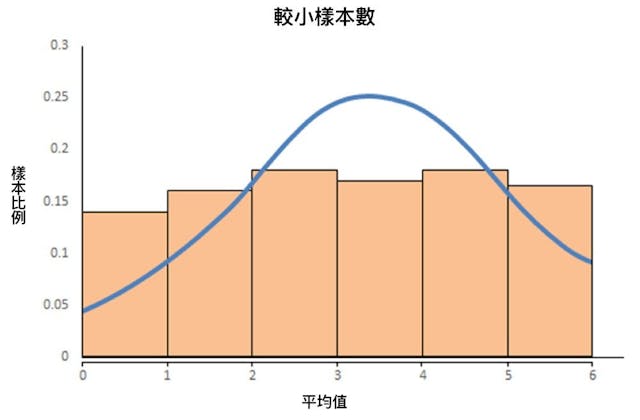
每個樣本都有自己不同的組成結構,每10次投擲的平均值,可以拉成一條10次移動平均線。當然閣下也可以投擲20次,50次,100次,200次,250次的平均值來拉出一條平均線。中央極限定理告訴我們,當樣本數愈多,平均值分布會愈接近常態分布。(筆者按:不過,大量的數據及實驗證明偏離常態分布的情況存在,極大值及極小值出現的機率大約是20%,符合巴瑞圖法則,又或俗稱80/20法則,所以最終形態是呈非常態分布。惟在日後的文章我會指出,即使呈非常態分布,傳統的統計學方法仍是合適的方法去解讀數據。)
回歸的應用
很多朋友對回歸均值的理解都有一定程度的偏差,筆者在其他平台的多篇分析文章,都指出2017年第四季的恆生指數偏離200天移動平均線甚遠,最終在2018年偏離達21.1% 而出現急速回吐。惟當時坊間很多朋友參考筆者的分析時都不甚了解,囫圇吞棗!有一份財經報章的研究員在媒體解讀筆者的分析文章時,指出大市一定要回至200天線,而當時的200天線是26600點。回歸均值不應是一條死線,以擲骰子為例,如果投擲得出多次數字1,我們會期望下一次擲出大於1的機率,會高於擲出數字1;就算是2,都已是回歸的表現。最終2月時回歸至偏離4%大市便喘定反彈,如果認為一定回歸200天線,而看空大市至非要觸及200天線不可,那便要面對大幅虧損了。
擲骰子的回歸操作,較易處理,因為沒有數字大於6或小於1。但在股市卻不一樣,以200天線為例,從以往的數據看,偏離18%,便很大機會出現回歸,是次最終偏離21.1%,如在偏離18% 時便看空大市,便要有捱價的準備!中央極限定理告訴我們,大市最終都會有回歸傾向,維持極值的時間不會太長。很多朋友在操作期權時,若大市出現超買/超賣的情況,都會用極短時間值的期權來操作。但按筆者的統計,在向心系統的分析中,周線出現超賣,反彈時出現回歸趨勢,都要花一定時間!以由超賣的狀態反彈25% 去修正超賣的情況下,花一周便成功達標的機率只有40%左右,反而2周達標的機率有55%,而4周內可以達標的機率達72%!筆者在期權操作上,曾有一段時間都會採用末日LONG的形式,貪其本小利大的可能性;惟勤做數據後,發現若用有足夠時間值的,反而更能提供高成功率,如能組成負值價差組合,便更是立於不敗之地。所以應用回歸均值概念時,既不可把均值看成死線,也要有足夠時間,讓回歸的趨勢發生。
市場的秩序就是混沌
要完全精確預測市場是不可能的,初始條件的偏差對後續的發展影響甚大。美國數學家兼氣象學家,愛德華‧羅倫茲,以蝴蝶效應描繪一隻蝴蝶在亞馬遜森林拍動翅膀,最終會令地球另一邊出現颶風!正是描述了初始條件對後續發展的重要性。但這還只是表述了事件的初始條件而已,而非在計量分析中,以量子力學的角度去理解大市。海森堡測不準定理(Heisenberg uncertainty principle)指出我們永遠無法同時完全確定粒子的位置及動量。我們可以在這一秒知道大市的收市價,以及一分鐘後的收市價,並能計算出這一分鐘的升跌幅,但卻不能預測在追一分鐘內出現的震盪!
計量分析,便是認知不能預測路徑的事實,即使最終回歸均值,其路徑都不可預測,所以計量分析便是用機率分布,或稱為機率雲來描述市場的狀態!筆者用的向心系統,便正是以機率分布來分析大市,同時也是用機率分布來推算結算價,以制定出較大成功機率的操作手法。






































