新年伊始,萬象更新。祝願各位灼見名家的讀者,今年百尺竿頭,更進一步。早前以歷史發展時序,把效率市場學說由誕生開始,至後來慢慢分家作介紹。計量分析以效率市場學說為基礎獨立出來。讀者可按圖索驥,慢慢學習。有些讀者認為筆者的文章太艱深難明,本篇是計量分析基本功最後一篇,筆者會用更淺白的文字說明。
今天介紹的人物是本華曼德博(Benoît B. Mandelbrot),筆者前文已提及這位數學及物理學大師,其研究對近代計量分析有關鍵作用,而他的徒弟費馬(Eugene Fama),更提出效率市場學說。不過據說,大師畢生未有以投資為業,只是單純有興趣研究市場與物理學關係。
大部分的博士學位, Ph.D.指的是Doctor of Philosophy,有萬事萬物最終都歸為哲學之意,曼德博便是以物理學來解釋世上萬事萬物。筆者在前文提及班佛定律(Benford’s Law),1.出現的機率最高,其次是2.之後漸減,這跟傳統的機率論,每一個數字出現的機率一樣是不同的。從班佛的研究,認為班佛定律可應用於物理學、社會學、語言學三個領域範疇!James Simons早期的研究便是用上齊夫定律在語言學中的發現,再配合馬可夫鏈(Markov Chain)發展出來。齊夫定律在曼德博的年代尚未完善,不少學者視為奇怪的計算方法,始終傳統的統計學及機率論已深入民心。曼德博在研究的過程中很快便找到改良計算公式的方法,亦以此完成其博士論文,更在未有任何指導教授下,獨力完成博士論文,在當時而言屬十分罕有。
從英國海岸線到股市
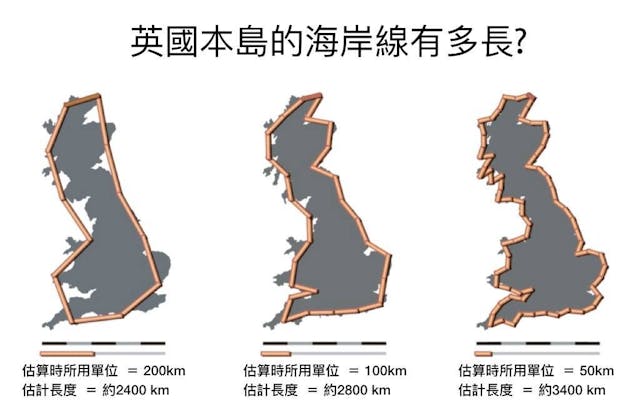
曼德博以齊夫定律為基礎,理解數字出現的機率並不平均。實際情況是某些數字出現的機率遠高於其他數字,令數字的分布呈折線形而非平滑平均的分布。他稱這種分布形態為碎形幾何(Fractal Geometry)。曼德博發現大自然裏有各種隨機模式。在1967年,他發表的海岸線悖論(Coastline Paradox)震驚學術界,雖已是50年前的論文,但至今其想法仍相當前衛,亦把奧地利學派的循環理論與物理學及動能分析融會貫通在一起。曼德博以英國本島的海岸線有多長為題展開探討。這個問題看似簡單,以現時的科技要精準量度亦仿似不難,但實際上卻絕不簡單,如果你用公里為量度單位,跟用米來做量度單位,得出來的結果便天差地遠,如果用厘米,差別便更大。海岸線是彎彎曲曲綿延不絕的,餘此類推,你永遠沒有辦法得到最精確的數字!曼德博提出,海岸線也好,其他事物也好,大都存有自相似性(Self-similarity)—即可以從零件中,透視出整體,而零件的零件也可透視出相似特性。
以股市為例,用秒圖來看,數分鐘便會出現細波幅橫行,急升,之後橫行,再急跌。這些分鐘為元件,累計下來便形成小時圖,而每數小時,便出現同樣走勢。每一段的波幅變化均有韻律,但長度不一;而每一個單元均相似卻非完全相同,主因是每時每刻都受到隨機因素所影響!
由2008年至今來看,恒生指數由低位橫行,再急升至23000點水平,之後較長時間橫行至2011年下跌,便是曼德博所指的生成元。2012年後橫行,再於2015年急升,2016年下跌,是另一個生成元。2017年上半年,是高位整固,步入7月後再升,可預示未來將出現一次調整,之後便可再闖高位。筆者在2016年12月舉行的2017年港股走勢講座中,已指出按波幅來看碎形模型,2017年並不具備2007/1997年等大幅急升後急跌的條件,大市目標以25,000/28,000/31,000點為阻力。筆者沒有水晶球,只是應用了曼德博的碎形理論及了解碎形中的不同波幅變化而已。
從曼德博的研究中,可見主要趨勢是以碎形分布形式重現走勢,而隨機現象只是在每時每刻影響一點波動性,一點時間性而已,並不會影響、終止主要趨勢!隨機現象有時沉靜,有時狂野,而其出現的頻率亦是有碎形分布的特性。2017年恒指的平均月波幅很細,表示2017年的隨機性非常沉靜,同時也預示了2018年/2019年隨機性會非常狂野,出現20%,甚至30%的月波幅的機率極高。
筆者有幸以專欄作家的身份參與灼見名家投資論壇,屆時會用碎形分布跟大家暢談大市2018年的走勢分析。








































