筆者青少年時期為基督徒,初信時曾在教會研討一個問題:如果沒有天堂,你還是否持守信仰?最後的結論是:天堂的福份是無限大的,今世持守的付出只是有限的時間、有限的付出。如沒有天堂,損失有限;如一旦有天堂,則以有限換取無限,值博率無限大。
首個提出這條命題的,便是今天文章的主角巴斯卡(Blaise Pascal)。他在名著《沉思錄》中以數學來論證信仰,發展出期望值理論(mathematical expectation)。假設你承認自己不知道上帝是否存在,因此對上帝存在與上帝不存在這兩個命題,你都認為有50%機會成立,那麼要決定對信仰是否虔誠時,該如何抉擇?
如何分配賭金?
有指巴斯卡對期望值的定義,成為日後賽局理論的基礎。巴氏年輕時是一位虔誠的信徒,但為了討生活,便受一位嗜賭的朋友委託去計算一條著名的「點數問題」──假設你置身一場賭局,賭博雙方贏的機率都一樣,而首個贏得某個點數的人便算贏了整場賭局。由於賭局在其中一方領先時被逼中止,那麼應如何分配賭金才公平?這情況跟股票期權相似,如深入價內的認購長倉(Long Call),由買入(Long)的一方決定何時行使,當一旦深入價內,便有誘因提早行使了。
要處理這條問題,答案要反映到在賭局中止時的優劣形勢下,雙方各自輸贏的機率。巴氏未能單獨解決問題,於1654年與另一位偉大的數學家費馬(Pierre de Fermat)通信交流,成了數學史上著名的費馬通信。從書信中可見二人最終都各自建立了解決問題的算式,不過巴氏的比較簡單易明。以一場七戰四勝制的比賽來說明,現時A隊已連勝首2場,餘下的5場,每次的勝敗機率均是50%,如果A隊再勝3場,餘下2場已不用比了,因為B隊的勝負已不重要。
首先,B隊贏得餘下5場中的4場,只有五種可能性:BBBBB,BABBB,BBABB,BBBAB,BBBBA,要5場全勝,便只有BBBBB。把所有可能情況加起來,B隊可以反敗為勝的機率是6/32,大約19%,而A隊取勝的機率便是26/32,約81%,所以如現階段便終止賽事,這個機率便應是賭注的分配比例。
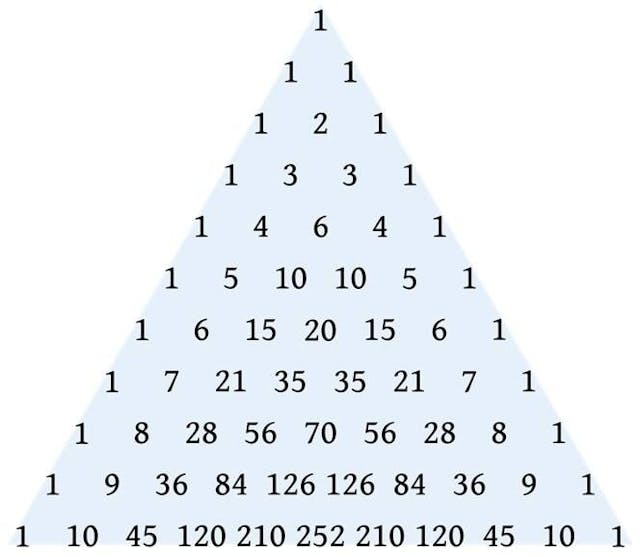
巴氏處理這個機率問題的方法,全靠他的巴斯卡三角形。事實上,這項成就早在1050年已由中國數學家賈憲完成,甚至1570年卡丹諾(Cardano)都曾提出這個計算方法。但把這個計算方法由理論發展到實務操作,卻是由巴斯卡帶進機率理論中完成,所以後世把功勞都歸於巴氏。
計量分析中不少理論基礎都與中國古代數學家有關,但當年只流於理論階段,未能發展至具實用性,身為中國人實在感到很可惜。這可能跟中國傳統文化要明心見性,多於發展實用科技有關。這並不反映中國人的能力較差,只是文化不同,年輕人盲目崇洋時,可曾思考西方文化亦有其不足之處?以近年港人喜愛日本文化為例,日本出品,認真用心,可是近月來不時爆出日企造假問題,日本在職人士過勞死亦時有所聞,我們可不能單單擁抱美好的片面,而忘記了文化與民族的發展方是一個整全體系。
大數據是萬能?
筆者以巴氏三角形來處理AB隊的計算問題。現時剩下5場比賽,直接取三角形的第5列,B隊可能贏0, 1, 2, 3, 4, 5場的方式有下列數種:1 5 10 10 5 1,即贏0場的機率是1,而贏5場的機率也是1,而贏2場及3場的方式則有10種,比贏1場及4場的機率多1倍。
當你懂得應用巴氏三角形,你便會發現用途非常廣泛。筆者在期權操作中,多以組成牛跨或熊跨來操作,多於把建立的裸頭好倉或淡倉直接平倉,也是因直接平倉要付出過大的期望值虧損,而牛跨及熊跨更能賺取獲利機會有關。1992年澳洲有幾位投機者,發現美國維吉尼亞州的大樂透的設定出錯。這個由1到44號組成的六個號碼組合,合共有7,059,052種數列,但頭獎彩金累積到2,700萬美元,再加上二獎、三獎等等,合共彩金為27,918,561元,回報比例是1:3.95。詳細故事發展不在此續談,最終結果是當局雖不服但仍要支付獎金。
近年坊間喜談大數據,如大家有讀過筆者於《信報》發表的文章,會發現筆者並不支持大數據是萬能的論點,下章再跟大家談談隨機情況下數據的處理方法。







































