恆生指數於2018年5月25日反覆下跌,不過就在15:27突然出現反彈。在跌市中出現反彈並不意外,只是在前一分鐘只有329張期指成交,5分鐘的平均成交量只是320張,而每分鐘平均波幅是22點,但在之後的這一分鐘內竟然有3,043張成交,波幅達到160點。這意味着在既無預兆也並非突發因素影響的情況下,成交及波幅都幾乎突增八倍。在市場中偶有出現這種突變情況,有時可能是因為俗稱為「肥手指」的錯盤情況,有時卻不能找出原因。
混沌理論建基於蝴蝶效應
法默(James Doyne Farmer)及諾曼‧派卡德(Norman Packard)花了15年時間去研究並創立了「非線形(nonlinear)動態操作」及「混沌(chaos)理論」, 他們的啟蒙老師就是鼎鼎大名的氣象學家羅倫茲(Edward Lorenz)。羅倫茲是早期運用電腦處理大量數據來預測天氣的科學家,有一次他用電腦去模擬天氣情況,輸入了風力及日照等多個參數然後得出結果。當時他是按電腦的初始設定,以小數點後六位數來作參考,不過這往往需時一整天才能得出答案。他試過改變運算模式,只取小數點後3位數來運算,希望可以更快得出答案。但即使所輸入的參數一樣,結果卻有天壤之別,因為當他採用小數點後三位數來計算,第四位數便會以四捨五入的形式來處理;同樣地,當採用小數點後六位數,電腦便會把第七位數用四捨五入的形式來處理。初時兩者只有小小差別,不過累積下來差別就很大。
羅倫茲於1972年向美國科學促進協會遞交了論文Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?,這就是今天著名的「蝴蝶效應」的出處。這效應是指當任何初始條件出現改變,後續的變化和影響均會很大,這也是「混沌理論」最初的理論基礎。
湍流時而波動時而沉寂
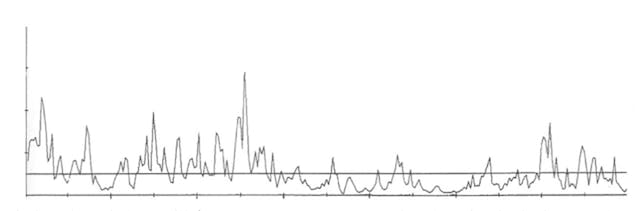
本華.曼德博的碎形研究則認為初始條件的改變是一種隨機因子,讓後續的變化出現很多不確定性,但大體上仍是會出現走勢重現的情況。空氣及水的流動都是以湍流(turbulence)為典型形態,參考本華‧曼德博被收錄在Statistical Models and Turbulence一書中關於空氣中湍流的論文,從下圖可見,橫線是平均值,湍流呈非常態分布,且在平均值上下穿梭的時間不長,偶爾更會出現極大值的情況,而且偏離均值甚遠。而且湍流的變化速度非常快,一時會劇烈波動,但一旦沉寂後卻又幾乎靜止。
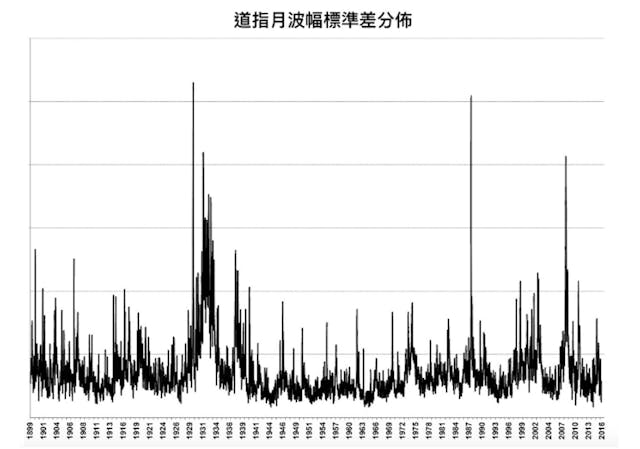
在金融市場湍流也同樣會出現這種情況。下圖是道指的月波幅標準差分布,從圖中可見每月的波動幅度相當大,而且不但呈非連續性,還具周期性,而其周期性跟奧地利學派的經濟循環理論相若。
學術理論與市場回報
1970年代是計量分析研究的黃金時代,本華‧曼德博在這年代發表了大量碎形研究。而羅倫茲亦進一步研究混沌理論,發現混沌理論中的隨機波動有一定的規律性,而某一些數字出現的機率明顯較高,他稱此為吸引因子(attractor)。
70年代末,愛德華‧索普(Edward Thorp)、法默及派卡德都把計量分析的理論實際應用於市場,創立了多個以計量分析為基礎的基金。與其一直停留於學術層面,不如用實際回報來說明現實。索普主要運用機率分布和回歸均值的方法,而法默及派卡德便是把吸引因子計算出來,由於市場有很大機率會出現吸引因子導向的數字,所以便有高勝算的機率。







































