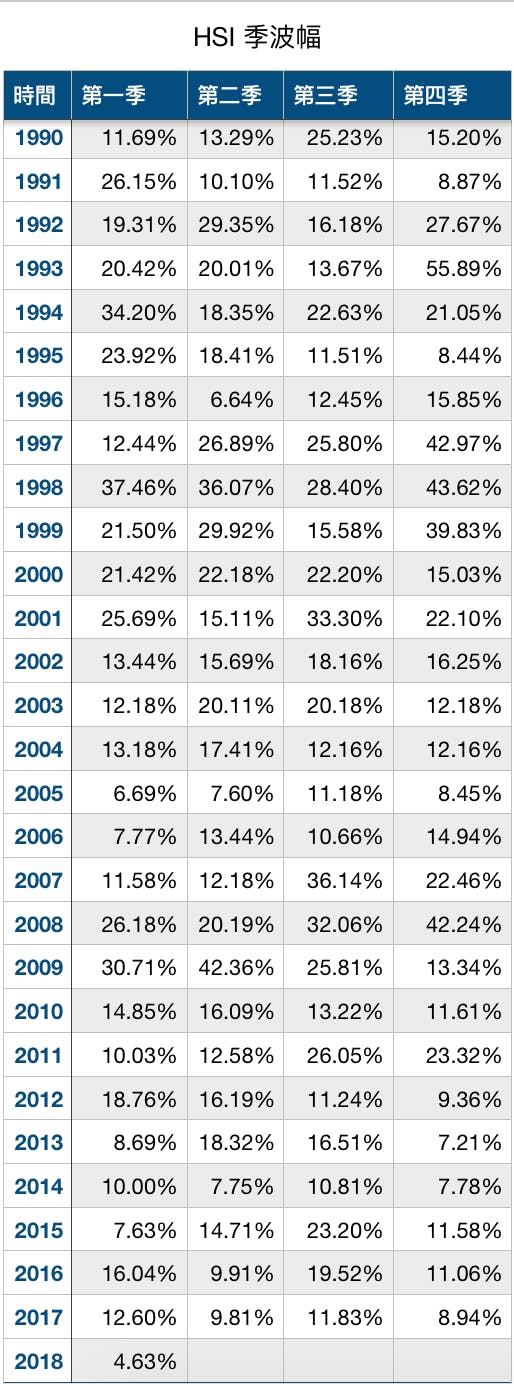
二次世界大戰時,由於空軍未算發達,德軍研發出著名的V2火箭隔海攻擊倫敦。按《邱吉爾傳》記載,當時V2的瞄準系統形同虛設,跟投石機的原理差不多,理論上落在倫敦任何一點的機率應一樣,但按當時統計,V2的落點明顯呈某種分布模式,而且有重複性,反映V2的落點並不完全隨機。如套用金融市場模型,巴楔利耶(Bachelier)認為股價走勢應呈常態分布,而在分布內將完全隨機。奧斯本(Osborne)則認為股價的升跌,並不是每次加1點或跌1點,而是以百分比的數值出現。筆者成為專欄作家之前,香港市面仍討論每月波幅多少點,大戶才夠深度操作,直至筆者發表了多篇波幅理論及公開了波幅計算,大家才開始轉用百分比來衡量波幅值,對香港市場因筆者專欄而出現的一點進步,筆者甚為欣喜。
隨機可以好狂野
按白努利(Bernoulli)的理論,只要你取樣夠多,便應呈常態分布,這便是前文提及的大數法則。但按本華‧曼德博 (Benoit Mandelbrot)的研究結果來看,大部分的機率分布,都不適用於大數法則。量子物理學大師費曼(Feynman),在其名著《量子物理學》中,舉了一個顯淺易明的例子:一名醉酒的士兵,拿着步槍定點射擊,而目標是一堵牆。當然每一發都是亂射的,有的射在正前方,有的射在兩邊很遠處,如按常態分布,出現在極遠處的機率應甚低,但事實上得到的結果遠比常態分布高。本華‧曼德博稱這現象為狂野隨機(wildly random),而這個情況,卻出現一種尾部肥大的現象,稱為巴瑞圖分布,反映隨機行為的表現,會出現一種有規律的分布模型。而隨機現象,只在分布模型的每時每刻出現,卻不會影響整體的運行走勢,就如用機器做出來的曲奇餅,受隨機因素影響,每一塊都略有不同,但大致上是一樣的。
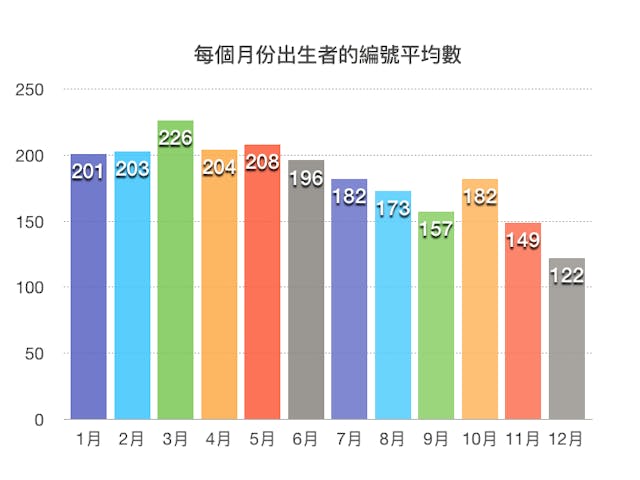
齊夫定律同樣影響隨機表現。1970年1月3日的《紐約時報》,便以齊夫定律探討了當時市民最關心的問題。當年美國正參與越戰,美國兵役登記局需要按一套機制抽出徵兵名單,以決定哪一些國民須入伍,為國捐軀!系統的運作模式如下:在366個彩蛋中抽出一個,每一個彩蛋都有一個日期,由1月1日至12月31日都有;同時亦有366個編碼,由1-366,假設抽出第一個彩蛋是4月1日,那便放在1號,而第二個抽出了5月1 日,便放在2號;號碼愈前的,便愈早安排接受軍訓,可預示也愈早被派往越南。
理論上這系統應是隨機的,每月的機率應一樣,但從圖表看,便了解事實上並非如此。1-5月出生的朋友,抽到的號碼平均值大於200,反而12月的人平均值是122,反映12月出生的人,更易提早上戰場,而死亡的機率也愈高!為什麼會出現如此情況呢?《紐約時報》便提供了有力的答案!
工作人員會把所有彩蛋放在一個大箱中,為免有遺漏,他們首先仔細順序排好次序,之後先把1月的彩蛋放入木箱,之後是2月,餘此類推。結果1-5月的彩蛋在木箱底部,12月的便在較上面,雖然會用木棍攪拌,但只會用順時針或逆時針打圈,不會上下顛倒,結果相同月份的只會橫移,在上面的仍是在上面,當工作人員伸手一抽,仍是12月的最先被抽中。
瞄準季波幅出手
2018年1月13日是筆者跟灼見名家合作開講座的日子,座中一位朋友問及季波幅問題。他計算出平均季波幅是12%左右,如果是這樣,倘若季中便升至12%,是否可以開淡倉呢?筆者當時回答:
一,假設這位朋友的計算正確,但滿足了季波幅12%,大市只是橫行沒有急跌,那雖然合乎你的計算值,但你的操作仍是失敗!
第二個情況,便是不同季度的波幅平均值並不一樣,每一季的波幅值都不一樣,首季波幅便跟第三季有明顯不同。其次,便是波幅有呈碎形分布,簡單一點來說,當月波幅變細的時候,最終將會出現大波幅。當大月波幅出現時,會出現(吸引)大波幅連續出現,所以大家會見到圖表所列,很多年份於第三季的波幅較大,而大波幅出現的月份並不是平均分布。而最終統計,十年甚至更長的時間,主要指數的波幅變化,均沒有遵從常態分布,極細及極大波幅出現的機率甚高,反而中波幅或波幅達平均值出現的機率較低。再推演深一層次理解,指數偏離平均線方是常態,在平均線上下穿梭才是罕有,但偏離至太遠的話,也是一個極端情況!這句話既說明了平均線不會是支持及阻力,也說明了偏離太多的情況下,是介入市場進行操作的適當時機。