前文談及奧斯本(Matthew Maury Osborne)發現的數列,連升後續升的機會略多於下跌,跟計算上50%的出現機率不同。事實勝於雄辯,計算上的結果跟大量數據得出來的實驗值不同,看似隨機的事情,卻暗藏規律。然而,這情況並不以一個固定比率重現,碎形理論大師,同時是效率市場說的創始人費馬(Eugene Fama)的老師本華‧曼德博 (Benoit Mandelbrot)便以碎形理論來解釋這些非線形的現象。

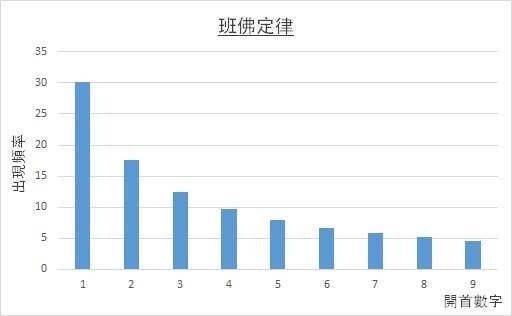
要簡單介紹碎形理論並不容易,我們不妨由簡單的科學定律入手。大家可曾發現,在圖書館供市民借閱的書籍,以1開頭的書頁比2開頭的書頁殘舊,餘此類推,另100頁的書頁比90頁的書頁殘破,不論書本被借閱的次數多寡,都會出現這種情況。這便是班佛定律(Benford’s Law),指在一堆數據中,數字出現的頻率並不一樣,1開頭的數約佔30%,2開頭的約佔18%,最後9開頭的約佔5%。一切自然產生的數據均會依從班佛定律,即使是股價的收市位,長年期累積大量數據,都會依從這定律,惟有人為操作的數據卻不一樣。
最經典的例子,是一位叫凱文‧勞倫斯的年輕企業家,以龐氏騙局手段集資,把投資者的錢,在銀行間轉來轉去,進行清洗黑錢,表面上卻是生意蒸蒸日上。調查人員搜集大量數據與班佛定律來比對,發現匯款的數字非自然產生,最後便啟動司法調查,勞倫斯在2003年被判處20年刑期。
如果數字真的是隨機出現,便不可能符合班佛定律。在已知有限的數據中,當數據量夠多,仍可按機率法則處理,例如擲公字或是擲骰子,但對於股市這種無窮無盡的數列,便不能用傳統的機率計算來取得解答。
極大的成就
雅各‧白努利(Jakob Bernoulli)在牛頓(Newton)及萊布尼茲(Leibniz)的微積分研究基礎上,得出極大量數值,並進行重複觀察/觀察後發現重複的情況(註:是哪一個意思呢?)。例如:擲公字,只擲10次,可能你會得到7次正面,3次反面,甚至連續10次正面都是有可能發生的,我們不能單以10次擲公字就斷然結果是非隨機的。筆者便曾以擲公字1,000次的結果,繪製成一張走勢圖,很多學生看到,都以為是某隻個股的圖表。即使筆者擲了1,000次,正面的結果大約是54%,而反面的結果是46%,期間還出現了多次連續5次正面及連續5次反面的結果,在機率而言都應是很罕見的,但在1,000次的投擲結果中,卻有13次連續出現5次同樣結果的記錄!

白努利花了20年時間去處理量化極大量數據的問題,今天我們稱為「大數法則」 。現時假設罐中有100顆彈珠,當中有60顆是白色,40顆是黃色,如果你只抽出其中50顆,出現58-62%的機率有多少?你能否抽出50顆便可以知道罐中的白黃比率是多少?大數法則會告訴你,當你抽出的數量「夠多」 ,你就可以接近確定那個答案。抽出數量愈多,得到的答案便愈接近準確,但只有抽出所有數量,最終才可得到100%肯定的答案!這既是近代演算法的理論基礎,事實上也是大數據的限制──就是永遠都不準確!
現實生活中,我們不可能檢驗數據幾百幾千次,結果往往把幾次的人生經驗,牢牢記在腦中,成了我們直覺判斷的依據,這種稱為賭徒謬誤。例如恆指連續3次,均是120個月出現一次見頂,便相信2017年10月會出現股災,而事實上,自1977年起,恆指便沒有出現股災了。又或者是近來沒有發生,就應該很快便會發生,這就像2009年便聽到道指快將出現調整,牛市才更健康一樣,結果是,一年又一年,盼了三年又三年。好事連連不代表將會遇到惡運,霉運蓋頂也不見得將會物極必反。在無盡的數據中,總有機會出現連續100次都擲到正面的,如果你剛好在其中,數到第10次,便期望下一次將會擲出反面,這種只是賭徒謬誤而已。香港坊間有一位名咀,在2017年1月便認為快將跌市,結果一年過去都未曾言中,這不正是說明什麼叫「不學無術」嗎?








































