從前文中大家可以了解到不是所有機率都可以計算出來的,所以才會有計算機率及主觀機率的分別。但有一些機率是不明確的,例如:企業推出新產品,市場反應和消費者的接受程度如何?這些幾乎是不可能準確預測到的。經濟學家法蘭克‧奈特 (Frank Knight) 把這種連主觀預測都難以判斷的情況定義為「奈氏不確定性」(Knightian Uncertainty);把能夠分配的機率狀況定義為「風險」(Risk);而連機率如何計算都不清楚的情況則被定義為「不確定」(Uncertainty)。奈特主張大部分涉及經濟的狀況都屬於不確定性。(筆者按:自發展碎形理論後,擅長物理學的計量分析大師都會定義為「風險」,主因是用物理學的量子模型可以大概可估算出機率分布。)
如果用「賽局理論」(Game Theory) 來說明小中取大原則,大家會更明白應該如何應用。談到賽局理論,一般人可能會想起納殊 (John Nash),又或是《有你終身美麗》(A Beautiful Mind)這套電影。但真正創造賽局理論的,其實是納殊的老師:美國一代天才數學家──馮‧紐曼 (Von Neumann)。如非早逝,學界幾乎可以肯定他是另一位愛因斯坦級的天才。(如大家有意進一步認識這位天才,筆者介紹大家研讀由左岸文化出版的《囚犯的兩難:賽局理論與數學天才馮紐曼的故事》一書。)紐曼於1944年刊載的〈賽局理論與經濟行為〉中提倡將人類所有行為視為賽局的理論,從自利的心態出發,配以不用的心計策略切入理論。參與者作出選擇時是會按着各自的利益來考慮(當然不是所有參與者都具理性,部份參與者不完全用理智去考慮自身利益),而由於遊戲是多方互動,所以參與者行動之先必須考慮他人的選擇,所以自身的決定也會受其他玩家的決定所影響。
大市可操作 不可預測
首先從二人博奕開始思考,參加者只有兩位,而不論結果如何,一位玩家的獲利就等同另一位玩家的損失,因此利益的總和必然是0。情況便跟期指一樣,當你買了期指獲利,便必有另一位對家出現同樣的損失。為了方便理解,筆者用列表形式說明:現時玩家甲可以用策略A、B和C,而玩家乙就可以用策略D、E和F來應對。
以下是玩家甲,採用策略後可能出現的結果:
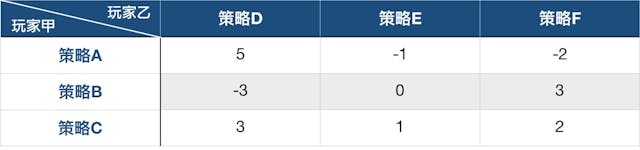
如玩家甲採用策略A會得到5分,而同時代表玩家乙會失去5分。如果大家作為玩家甲,當然希望得到最高分數和最大利益。但同時玩家乙也需提防對方採用哪一種策略會帶來最大的風險。如玩家乙認定玩家甲是高風險玩家,便會以策略F來應對,屆時便可以在玩家甲身上得到2分。
這種零和情況,高度適用於理解期權操作:如採用先Short後Long的方法,雖然會為己方帶來小利,卻有極大風險,同時有機會令對家賺取厚利。所以可說,先Short後Long的方法是在對家能獲取最大利潤的情況下才會考慮的操作方法!所以教導大家採用這種操作方式的,如非蠢才或不理智的人士,便是希望閣下在零和遊戲中輸更多,好讓對家獲利更豐!居心何在,大家可自行思考。
很多朋友參加筆者的講座,都會期望我估計一下大市。但以零和遊戲為例,當你估算別人行動時,別人也在估算你,是否猜中根本難料。紐曼在這方面提供了一條出路,這亦是筆者所提倡:「大市可操作,而不可預測」的精神。所謂的小中取大準則,就是看看採用某行動的最低保證獲利有多少。用上表來理解,玩家甲採用策略C時最低獲利是1分,而最高獲利是3分,平均獲利是2分。只要持續用同一個方法,雖然沉悶,卻可穩定致勝。
當然,用期權時即使先Long後Short都不可能零風險,但輸的是有限,回報卻往往比所付出的期權金多出數倍,可理解為輸時是-1,而賺時卻是2、 3甚至是4到5分。雖未可做到任何情況下皆獲利,但配合價位的分布來計算機率,提高操作成功率,便可達至平均值是正數的結果。之後只要持之以衡,便可穩定獲利。







































